मुआवजा प्रमेय: कार्य करना, उदाहरण और इसके अनुप्रयोग

नेटवर्क सिद्धांत में, इसकी एक शाखा में प्रतिबाधा के भीतर परिवर्तन के प्रभाव का अध्ययन करना या जानना बहुत महत्वपूर्ण है। तो यह सर्किट या नेटवर्क के संबंधित धाराओं और वोल्टेज को प्रभावित करेगा। तो मुआवजा प्रमेय का उपयोग नेटवर्क के भीतर परिवर्तन को जानने के लिए किया जाता है। इस नेटवर्क प्रमेय बस ओम के नियम की अवधारणा पर काम करता है, जिसमें कहा गया है कि, जब भी पूरे रेसिस्टर में करंट की आपूर्ति की जाती है, तो कुछ मात्रा में वोल्टेज रेसिस्टर पर गिर जाएगा। तो यह वोल्टेज ड्रॉप वोल्टेज स्रोत का विरोध करेगा। इस प्रकार, हम वोल्टेज स्रोत के विपरीत रिवर्स पोलरिटी में एक अतिरिक्त वोल्टेज स्रोत कनेक्ट करते हैं और परिमाण वोल्टेज ड्रॉप के बराबर होता है। यह लेख a . के एक सिंहावलोकन पर चर्चा करता है मुआवजा प्रमेय - अनुप्रयोगों के साथ काम करना।

मुआवजा प्रमेय क्या है?

नेटवर्क विश्लेषण में क्षतिपूर्ति प्रमेय को इस प्रकार परिभाषित किया जा सकता है; एक नेटवर्क में, कोई भी प्रतिरोध एक वोल्टेज स्रोत के साथ प्रतिस्थापित किया जा सकता है जिसमें शून्य आंतरिक प्रतिरोध और वोल्टेज ड्रॉप के बराबर वोल्टेज शामिल होता है, क्योंकि इसके पूरे प्रवाह में प्रवाहित प्रतिरोध होता है।

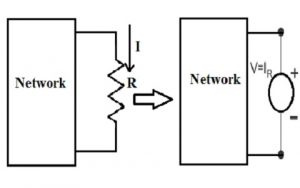
आइए मान लें कि वर्तमान 'I' का प्रवाह उस 'R' में है अवरोध और वोल्टेज कम हो जाता है क्योंकि इस प्रवाह के प्रवाह को रोकनेवाला (V = I.R) है। क्षतिपूर्ति प्रमेय के आधार पर, इस प्रतिरोधक को वोल्टेज स्रोत के माध्यम से प्रतिस्थापित किया जाता है जो वोल्टेज उत्पन्न करता है और जिसे नेटवर्क वोल्टेज दिशा या वर्तमान दिशा के विरुद्ध निर्देशित किया जाएगा।

मुआवजा प्रमेय हल की गई समस्याएं

मुआवजा प्रमेय की उदाहरण समस्याएं नीचे दी गई हैं।

उदाहरण 1:

निम्नलिखित सर्किट के लिए

1) । एक बार प्रतिरोध 4Ω हो जाने पर AB शाखा में धारा प्रवाह ज्ञात कीजिए।
2))। एक बार प्रतिरोध 3Ω को 9Ω से बदलने पर क्षतिपूर्ति प्रमेय के साथ AB शाखा में धारा का प्रवाह ज्ञात कीजिए।
3))। मुआवजा प्रमेय की पुष्टि करें।

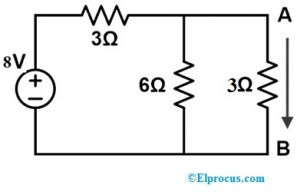
समाधान:

जैसा कि उपरोक्त सर्किट में दिखाया गया है, दो प्रतिरोधों जैसे 3Ω और 6Ω समानांतर में जुड़े हुए हैं, और यह समानांतर संयोजन भी श्रृंखला में 3Ω रोकनेवाला के साथ जुड़ा हुआ है, तो समान प्रतिरोध होगा;

री1 = 6 || 3 + 3 => (6×3/6+3) + 3
= (18/9) + 3 => 2+3 = 5 .

पर आधारित ओम का नियम ;

8 = मैं (5)
मैं = 8 5
मैं = 1.6 ए

अब, हमें AB शाखा में धारा का प्रवाह ज्ञात करना है। इस प्रकार, वर्तमान विभक्त के नियम के आधार पर;

मैं' = 1.6 (6)/6+3 => 9.6/9 = 1.06ए

2))। अब हमें 3Ω रेसिस्टर को 9Ω रेसिस्टर से बदलना होगा। मुआवजा प्रमेय के आधार पर, हमें श्रृंखला के भीतर 9Ω प्रतिरोधी के साथ एक नया वोल्टेज स्रोत शामिल करना चाहिए और वोल्टेज स्रोत मान है;

वीसी = मैं' Z

कहाँ पे,

Z = 9 - 3 = 6 और I' = 1.06 A.

वीसी = (1.06) x 6 = 6.36V

वीसी = 6.36 वी

संशोधित सर्किट आरेख नीचे दिखाया गया है।

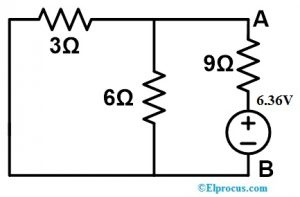
अब हमें तुल्य प्रतिरोध ज्ञात करना है। तो, 3Ω और 6Ω जैसे प्रतिरोधक केवल समानांतर में जुड़े हुए हैं। उसके बाद यह समानांतर संयोजन केवल 9Ω रोकनेवाला द्वारा श्रृंखला में जुड़ा हुआ है।

अनुरोध = 3||6+9

अनुरोध = (3×6||3+6) +9

अनुरोध = (18||9) +9

अनुरोध = (2) +9

अनुरोध = 11ohms

ओम के नियम पर आधारित;

वी = I एक्स आर

6.36 = I (11)

मैं = 6.36 11

I = 0.578 ए

इस प्रकार, क्षतिपूर्ति प्रमेय के आधार पर; धारा के भीतर परिवर्तन 0.578 ए है।

3))। अब हमें निम्नलिखित परिपथ में 9Ω प्रतिरोधक के साथ धारा के प्रवाह की गणना करके क्षतिपूर्ति प्रमेय को सिद्ध करना है। तो, संशोधित सर्किट नीचे दिया गया है। यहां, 9Ω और 6Ω जैसे प्रतिरोधक समानांतर में जुड़े हुए हैं और यह संयोजन केवल 3Ω रोकनेवाला द्वारा श्रृंखला में जुड़ा हुआ है।

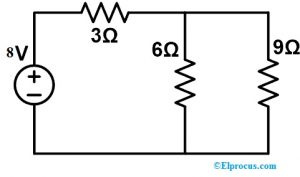
आरईक्यू = 9 | | 6 + 3

आरईक्यू = (6×9 | 6 + 9) + 3

आरईक्यू = (54 | 15) + 3

आरईक्यू = 45+54/15 => 99/15 => 6.66ohms

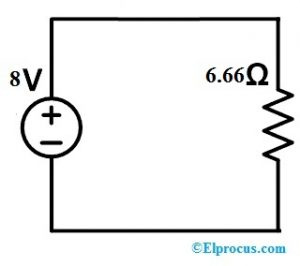
ऊपर के सर्किट से

8 = मैं (6.66)

मैं = 8 6.66

मैं = 1.20ए

वर्तमान विभक्त नियम के आधार पर;

मैं '' = 1.20 (6)/6+9

मैं'' = 1.20 (6)/6+9 =>7.2/15 =>0.48ए

मैं = मैं' - मैं'

I = 1.06-0.48 = 0.578A

इसलिए, मुआवजा प्रमेय साबित होता है कि वर्तमान के भीतर परिवर्तन की गणना उस प्रमेय से की जाती है जो वास्तविक सर्किट से मापी गई धारा के भीतर परिवर्तन के समान है।

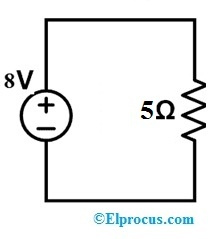
उदाहरण 2:

निम्नलिखित सर्किट ए और बी के दो टर्मिनलों में प्रतिरोध मान को 5ohms में संशोधित किया जाता है तो मुआवजा वोल्टेज क्या है?

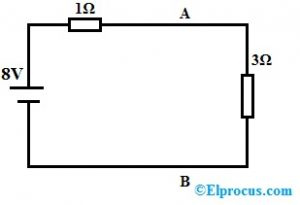
उपरोक्त सर्किट के लिए, सबसे पहले, हमें KVL लागू करने की आवश्यकता है

-8+1i+3i = 0

4i = 8 => मैं = 8/4

मैं = 2ए

Δआर = 5Ω - 3Ω

आर = 2Ω

मुआवजा वोल्टेज है

वीसी = मैं [ΔR]

वीसी = 2×2

वीसी = 4 वी

एसी सर्किट में मुआवजा प्रमेय

निम्नलिखित एसी सर्किट के भीतर वर्तमान प्रवाह परिवर्तन का पता लगाएं यदि एक 3 ओम अवरोधक को क्षतिपूर्ति प्रमेय के साथ 7 ओम अवरोधक के माध्यम से बदल दिया जाए और इस प्रमेय को भी साबित करें।

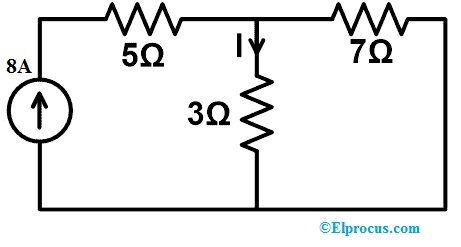
उपरोक्त सर्किट में केवल प्रतिरोधक और साथ ही अलग-अलग वर्तमान स्रोत शामिल हैं। इस प्रकार, हम इस प्रमेय को उपरोक्त परिपथ में लागू कर सकते हैं। तो इस सर्किट को करंट सोर्स के जरिए सप्लाई किया जाता है। तो अब हमें की मदद से 3Ω रेसिस्टर की पूरी शाखा में करंट का प्रवाह ज्ञात करना होगा केवीएल या केसीएल . हालाँकि, करंट के इस प्रवाह को वर्तमान विभक्त नियम का उपयोग करके आसानी से पाया जा सकता है।

तो, वर्तमान विभक्त नियम के आधार पर;

मैं = (8(7)/7+3) ए => 56/10ए => 5.6ए।

3ohms रेसिस्टर वाले वास्तविक सर्किट में, उस शाखा में करंट का प्रवाह 7A होता है। तो हमें इस 3ohm रेसिस्टर को 7ohm से बदलना होगा। इस बदलाव के कारण उस शाखा में करंट का प्रवाह भी बदल जाएगा। तो अब हम मुआवजे के प्रमेय के साथ इस मौजूदा बदलाव को पा सकते हैं।

उसके लिए, हमें केवल वर्तमान स्रोत को ओपन-सर्किट करके और वोल्टेज स्रोत को शॉर्ट-सर्किट करके नेटवर्क के भीतर सभी उपलब्ध स्वतंत्र स्रोतों को हटाकर एक मुआवजा नेटवर्क तैयार करना होगा। इस सर्किट में, हमारे पास केवल एक ही करंट सोर्स होता है जो एक आदर्श करंट सोर्स होता है। इसलिए, हमें आंतरिक प्रतिरोध को शामिल करने की आवश्यकता नहीं है। इस सर्किट के लिए, अगला संशोधन जो हमें करने की आवश्यकता है वह है एक अतिरिक्त वोल्टेज स्रोत को शामिल करना। तो यह वोल्टेज मान है;

सीवी = मैं Z => 7 × (7 – 3)

सीवी = 7 × 4 => 28 वी

अब वोल्टेज स्रोत के साथ मुआवजा सर्किट नीचे दिखाया गया है।

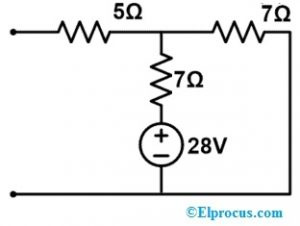
इस सर्किट में केवल एक लूप शामिल है जहां 7Ω शाखा में वर्तमान आपूर्ति हमें वर्तमान परिवर्तन का प्रवाह प्रदान करेगी यानी, (∆I)।

I = VC (7+7) => 28 ÷ 14 => 2 A

इस प्रमेय को सिद्ध करने के लिए, हमें नीचे दिए गए परिपथ में दर्शाए अनुसार 7Ω के प्रतिरोधक को जोड़कर परिपथ के भीतर धारा के प्रवाह का पता लगाना होगा।

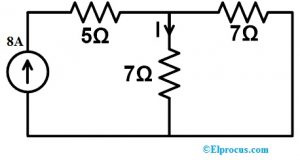
मैं” = (8 (7)) (7 + 7)

मैं” = 56 14

मैं” = 4 ए

अब वर्तमान विभक्त नियम लागू करें;

करंट में बदलाव का पता लगाने के लिए, हमें इस करंट को उस करंट से घटाना होगा जो मूल नेटवर्क से होकर गुजरता है।

मैं = मैं - मैं'

I = 7 – 4 => 3 ए

अतः क्षतिपूर्ति प्रमेय सिद्ध होता है।

हमें मुआवजा प्रमेय की आवश्यकता क्यों है?

• मुआवजा प्रमेय बहुत उपयोगी है क्योंकि यह नेटवर्क के भीतर परिवर्तन के बारे में जानकारी प्रदान करता है। यह नेटवर्क प्रमेय हमें नेटवर्क की किसी भी शाखा के भीतर सटीक वर्तमान मूल्यों का पता लगाने की अनुमति देता है, जब नेटवर्क को एक ही चरण में किसी विशिष्ट परिवर्तन के लिए सीधे प्रतिस्थापित किया जाता है।
• इस प्रमेय का उपयोग करके हम एक नेटवर्क के तत्वों के भीतर सूक्ष्म परिवर्तनों का अनुमानित प्रभाव प्राप्त कर सकते हैं।

लाभ

मुआवजा प्रमेय के लाभ निम्नलिखित को शामिल कीजिए।

• मुआवजा प्रमेय नेटवर्क के भीतर परिवर्तन के बारे में जानकारी प्रदान करता है।
• यह प्रमेय ओम के नियम की मूल अवधारणा पर कार्य करता है।
• सर्किट के भीतर प्रतिरोध मान को समायोजित करने के बाद यह वोल्टेज या करंट के भीतर परिवर्तनों की खोज करने में मदद करता है।

अनुप्रयोग

मुआवजा प्रमेय के आवेदन निम्नलिखित को शामिल कीजिए।

• विद्युत नेटवर्क तत्वों के भीतर अनुमानित छोटे परिवर्तन प्रभाव प्राप्त करने के लिए इस प्रमेय का अक्सर उपयोग किया जाता है।
• यह विशेष रूप से ब्रिज नेटवर्क की संवेदनशीलता का विश्लेषण करने के लिए बहुत उपयोगी है।
• इस प्रमेय का उपयोग उन नेटवर्कों का विश्लेषण करने के लिए किया जाता है जहां शाखा तत्वों के मूल्यों को बदल दिया जाता है और ऐसे मूल्यों पर सहिष्णुता प्रभाव का अध्ययन करने के लिए भी प्रयोग किया जाता है।
• यह आपको किसी भी नेटवर्क शाखा के भीतर सही वर्तमान मूल्यों को निर्धारित करने की अनुमति देता है, जब नेटवर्क को सीधे एक ही चरण में किसी विशिष्ट परिवर्तन के लिए प्रतिस्थापित किया जाता है।
• यह प्रमेय नेटवर्क विश्लेषण के भीतर सबसे महत्वपूर्ण प्रमेय है जिसका उपयोग विद्युत नेटवर्क की संवेदनशीलता की गणना और विद्युत नेटवर्क और पुलों को हल करने के लिए किया जाता है।

इस प्रकार, यह मुआवजे का एक सिंहावलोकन है नेटवर्क विश्लेषण में प्रमेय - उदाहरण समस्याएं और उनके अनुप्रयोग। तो इस नेटवर्क प्रमेय में, किसी भी सर्किट में प्रतिरोध को वोल्टेज स्रोत द्वारा बदला जा सकता है, एक समान वोल्टेज होने पर जब वोल्टेज प्रतिरोध में बदल जाता है जिसे बदल दिया जाता है। यहाँ आपके लिए एक प्रश्न है, क्या है अध्यारोपण प्रमेय ?