मौलिक नेटवर्क प्रमेय नेटवर्क विश्लेषण में उपयोग किए जाने वाले विभिन्न प्रकारों में उपलब्ध हैं जैसे थेवेनिन, सुपरपोजिशन, नॉर्टन, प्रतिस्थापन, अधिकतम शक्ति हस्तांतरण, पारस्परिकता और मिलमैन के प्रमेय . प्रत्येक प्रमेय, उनके अपने अनुप्रयोग क्षेत्र होते हैं। इसलिए प्रत्येक नेटवर्क प्रमेय को समझना बहुत महत्वपूर्ण है क्योंकि इन प्रमेयों को विभिन्न परिपथों में बार-बार उपयोग किया जा सकता है। ये प्रमेय किसी दी गई स्थिति के लिए जटिल नेटवर्क सर्किट को हल करने में हमारी मदद करते हैं। यह आलेख नेटवर्क प्रमेय के प्रकारों में से एक पर चर्चा करता है प्रतिस्थापन प्रमेय - उदाहरण।
प्रतिस्थापन प्रमेय क्या है?
प्रतिस्थापन प्रमेय कथन है; कि जब भी पूरी ब्रांच में करंट या नेटवर्क में किसी भी ब्रांच में वोल्टेज का पता चलता है, तो ब्रांच को अलग-अलग एलिमेंट्स के कॉम्बिनेशन से बदला जा सकता है जो उस ब्रांच में समान वोल्टेज और करंट बनाएगा। दूसरे शब्दों में, इसे इस प्रकार परिभाषित किया जा सकता है; थर्मल वोल्टेज, साथ ही करंट, शाखा की तुल्यता के लिए समान होना चाहिए।
प्रतिस्थापन प्रमेय की अवधारणा मुख्य रूप से एक तत्व के दूसरे तत्व के साथ प्रतिस्थापन पर निर्भर करती है। यह प्रमेय कुछ अन्य प्रमेयों को सिद्ध करने में भी बहुत सहायक है। यद्यपि यह प्रमेय उस प्रमेय को हल करने के लिए लागू नहीं है जिसमें उपरोक्त दो स्रोत शामिल हैं जो न तो श्रृंखला में और न ही समानांतर में जुड़े हुए हैं।
प्रतिस्थापन प्रमेय की व्याख्या
प्रतिस्थापन प्रमेय को हल करने में शामिल चरणों में मुख्य रूप से निम्नलिखित शामिल हैं।
स्टेप 1: सबसे पहले, हमें सभी नेटवर्क तत्वों के वोल्टेज और करंट को खोजने की जरूरत है। सामान्य तौर पर, वोल्टेज और करंट की गणना ओम कानून की मदद से की जा सकती है, किरचॉफ कानून जैसे KVL, या KCL।
चरण दो: आवश्यक शाखा का चयन करें जिसे आप वोल्टेज स्रोत/प्रतिरोध और वर्तमान स्रोत जैसे किसी भिन्न तत्व के माध्यम से निकालना चाहते हैं।
चरण 3: प्रतिस्थापित तत्व का सही मान ज्ञात कीजिए बशर्ते कि वोल्टेज और करंट में परिवर्तन न हो।
चरण 4: सभी तत्वों के वर्तमान और वोल्टेज की गणना करके नए सर्किट की जांच करें और मूल नेटवर्क द्वारा इसका मूल्यांकन करें।
प्रतिस्थापन प्रमेय सर्किट आरेख
आइए हम निम्नलिखित परिपथ आरेख का उपयोग करके प्रतिस्थापन प्रमेय को आसानी से समझें। हम जानते हैं कि प्रतिस्थापन प्रमेय एक तत्व का दूसरे समकक्ष तत्व के साथ प्रतिस्थापन है। यदि नेटवर्क के भीतर किसी भी तत्व को वर्तमान स्रोत या वोल्टेज स्रोत के साथ प्रतिस्थापित/प्रतिस्थापित किया जाता है, जिसका वर्तमान और वोल्टेज पूरे या पूरे तत्व में पिछले नेटवर्क की तरह अपरिवर्तित रहेगा।
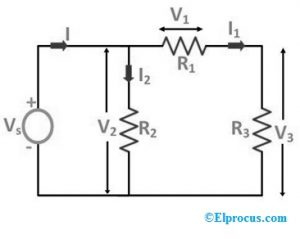
R1, R2 और R3 जैसे विभिन्न प्रतिरोध केवल वोल्टेज स्रोत से जुड़े होते हैं। पूरे सर्किट में बहने वाली धारा 'I' के प्रवाह को I1 और I2 में विभाजित किया जाता है, जहां 'I1' को पूरे 'R1' प्रतिरोध में आपूर्ति की जाती है और 'I2' पूरे R2 प्रतिरोध में प्रवाहित होता है जैसा कि सर्किट में दिखाया गया है। यहां, प्रतिरोध R1, R2 और R3 में वोल्टेज गिरता है, V1, V2 और V3 संगत रूप से होते हैं।
अब यदि 'R3' प्रतिरोध को 'V3' वोल्टेज स्रोत द्वारा प्रतिस्थापित किया जाता है जैसा कि नीचे दिए गए सर्किट आरेख में दिखाया गया है:
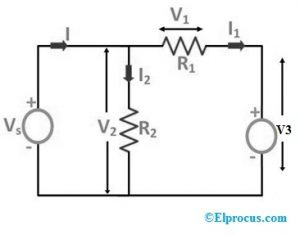
निम्नलिखित सर्किट आरेख में, 'R3' प्रतिरोध को उस तत्व 'I1' में करंट के प्रवाह से बदल दिया जाता है।
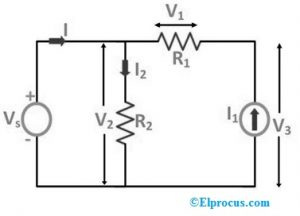
उपरोक्त दो मामलों से, यदि तत्व को करंट या वोल्टेज स्रोत से प्रतिस्थापित किया जाता है, तो सर्किट की प्रारंभिक स्थितियाँ नहीं बदलती हैं, जिसका अर्थ है कि पूरे प्रतिरोध में वोल्टेज की आपूर्ति और पूरे प्रतिरोध में करंट की आपूर्ति नहीं बदली जाती है, भले ही उन्हें दूसरे के साथ बदल दिया जाए। स्रोत।
उदाहरण समस्याएं
प्रतिस्थापन प्रमेय उदाहरण समस्याओं पर नीचे चर्चा की गई है।
उदाहरण 1:
सभी प्रतिरोधों के भीतर वोल्टेज और करंट की गणना करने के लिए प्रतिस्थापन प्रमेय के साथ निम्नलिखित सर्किट को हल करें।
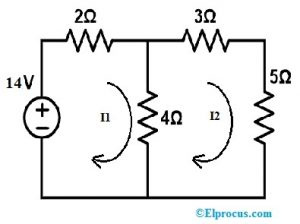
स्टेप 1:
सबसे पहले, उपरोक्त सर्किट में KVL को लूप1 पर लागू करें
14 = 6I1 - 4I2 ....(1)
उपरोक्त सर्किट में केवीएल को लूप 2 पर लागू करें
0 = 12I2 - 4I1
12 I2 = 4I1 => I1 = 3I2 ……….(2)
उपरोक्त समीकरण 1 में इस समीकरण 2 को रखिये।
14 = 6(3I2) - 4I2
14 = 18I2 - 4I2 =>14I2 => 1A
I2 = 1A
उपरोक्त समीकरण से-(2)
I1 = 3I2
हम जानते हैं कि I2 = 1A
I1 = 3A
चरण दो:
इस चरण में, हमें एक लूप बनाने के लिए लूप 1 शाखाओं को निकालना होगा।
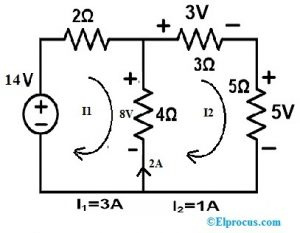
चरण 3:
हम 4Ω रेसिस्टर के स्थान पर करंट सोर्स/वोल्टेज सोर्स लगा सकते हैं। अब, हम एक वर्तमान स्रोत का उपयोग करेंगे।
सर्किट में पूरे लूप 2 में करंट का प्रवाह 1A है। इसलिए, हम शाखा को 1A वर्तमान स्रोत से प्रतिस्थापित करते हैं। नतीजतन, अवशिष्ट सर्किट नीचे दिखाया गया है।
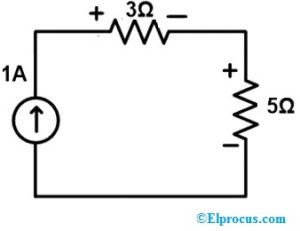
चरण 4:
इस चरण में, सभी तत्वों के वोल्टेज और करंट की जांच करने की आवश्यकता है। उपरोक्त सर्किट में सिंगल लूप यानी करंट सोर्स शामिल है। इस प्रकार, पूरे लूप में प्रवाहित धारा का मान वर्तमान स्रोत मान के समान है।
यहाँ, वर्तमान स्रोत मान 1A है। तो, 3Ω और 5Ω रेसिस्टर शाखाओं में करंट का प्रवाह 1A है जो मूल नेटवर्क के समान है।
का उपयोग करके ओम का नियम , 3Ω रोकनेवाला के पार वोल्टेज मान ज्ञात करें
वी = आईएस
वी = मैं एक्स आर
वी = 1 एक्स 3 => 3 वी।
इसी तरह, ओम के नियम का उपयोग करके, हमें 5Ω रेसिस्टर के आर-पार वोल्टेज मान ज्ञात करने की आवश्यकता है।
वी = आईएस
वी = मैं एक्स 5
वी = 1 एक्स 5 => 5 वी।
इस प्रकार, वर्तमान और वोल्टेज मूल नेटवर्क के समान हैं। तो, यह प्रमेय इस प्रकार काम करता है।
अब, यदि हम चरण 3 के भीतर वर्तमान स्रोत के स्थान पर वोल्टेज स्रोत चुनते हैं। तो इस स्थिति में, वोल्टेज स्रोत मान 4Ω प्रतिरोधी शाखा मान के समान होता है।
मूल नेटवर्क के भीतर 4Ω प्रतिरोधक शाखा में धारा का प्रवाह है
I1 – I2 => 3 – 1 => 2A
ओम के नियम के अनुसार;
4Ω रोकनेवाला पर वोल्टेज V = 2 x 4 = 8V . है
इसलिए, हमें नेटवर्क में वोल्टेज स्रोत को 8V से जोड़ने की आवश्यकता है और अवशिष्ट सर्किट नीचे दिए गए आरेख में दिखाया गया है।
वी = 2 एक्स 4 = 8 वी
इसलिए, हमें 8V वोल्टेज स्रोत को नेटवर्क से जोड़ने की आवश्यकता है और शेष सर्किट जैसा कि नीचे दिए गए चित्र में दिखाया गया है।
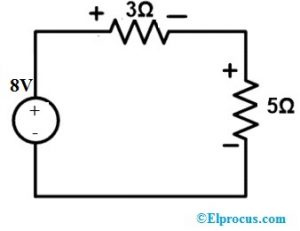
वोल्टेज और करंट को सत्यापित करने के लिए उपरोक्त लूप में केवीएल लागू करें।
8 = 3I + 5I => 8I
मैं = 1 ए।
ओम नियम का उपयोग करके, प्रतिरोधक 3Ω के आर-पार वोल्टेज की गणना इस प्रकार की जा सकती है;
वी = 1 × 3 => 3वी
इसी प्रकार, प्रतिरोधक 5Ω के आर-पार वोल्टेज है;
वी= 1 × 5 => 5वी
इस प्रकार, मूल नेटवर्क के रूप में प्रतिस्थापन के बाद वोल्टेज और करंट समान होते हैं।
उदाहरण 2:
आइए प्रतिस्थापन प्रमेय को लागू करने के लिए निम्नलिखित परिपथ लें।
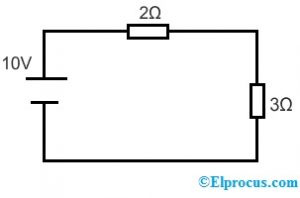
वोल्टेज डिवीजन रूलर के अनुसार, 2Ω और 3Ω प्रतिरोधों में वोल्टेज है;
3Ω रोकनेवाला पर वोल्टेज है
वी = 10×3/3+2 = 6वी
2Ω रोकनेवाला पर वोल्टेज है
वी = 10×2/3+2 = 4वी
पूरे सर्किट में करंट के प्रवाह की गणना I = 10/3+2 = 2A के रूप में की जाती है।
उपरोक्त सर्किट में, यदि हम 3Ω रेसिस्टर के स्थान पर 6Vवोल्टेज स्रोत को प्रतिस्थापित करते हैं तो सर्किट निम्न जैसा हो जाएगा।
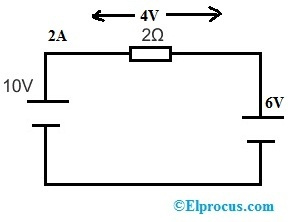
ओम के नियम के आधार पर, 2Ω रेसिस्टर में वोल्टेज और पूरे सर्किट में करंट का प्रवाह होता है
वी = 10-6 => 4वी
मैं = 10-6/2 = 2ए
यदि हम 3Ω रोकनेवाला के स्थान पर 2A धारा स्रोत को प्रतिस्थापित करते हैं तो परिपथ निम्न जैसा हो जाएगा।
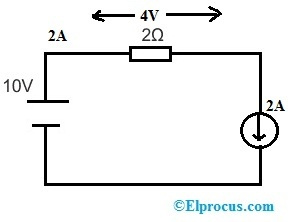
2Ω रेसिस्टर का वोल्टेज V = 10 - 3 * 2 => 4 V है और '2A' के करंट सोर्स पर वोल्टेज V = 10 - 4 => 6 V है। इसलिए पूरे सर्किट में 2Ω रेसिस्टर और करंट के वोल्टेज में बदलाव नहीं होता है।
लाभ
प्रतिस्थापन प्रमेय के लाभ निम्नलिखित को शामिल कीजिए।
- यह प्रमेय अवधारणा मुख्य रूप से एक तत्व के दूसरे तत्व से प्रतिस्थापन पर निर्भर करती है।
- यह प्रमेय सर्किट व्यवहार पर अंतर्ज्ञान प्रदान करता है और विभिन्न अन्य नेटवर्क प्रमेयों को सत्यापित करने में भी सहायता करता है।
- इस प्रमेय का उपयोग करने का लाभ यह है कि यह प्रमेय X और Y जैसे चरों के लिए सही मान प्रदान करता है जो प्रतिच्छेदन बिंदु से मेल खाते हैं।
सीमाओं
प्रतिस्थापन प्रमेय की सीमाएं निम्नलिखित को शामिल कीजिए।
- इस प्रमेय का उपयोग ऐसे नेटवर्क को हल करने के लिए नहीं किया जा सकता है जिसमें कम से कम दो या उससे अधिक स्रोत शामिल हों जो श्रृंखला/समानांतर के भीतर नहीं हैं।
- इस प्रमेय में, तत्व को प्रतिस्थापित करते समय, परिपथ का व्यवहार नहीं बदलना चाहिए।
अनुप्रयोग
प्रतिस्थापन प्रमेय के अनुप्रयोग निम्नलिखित को शामिल कीजिए।
- प्रतिस्थापन प्रमेय का उपयोग कई अन्य प्रमेयों को सिद्ध करने के लिए किया जाता है।
- यह प्रमेय गणित में समीकरणों के निकाय को हल करने में सहायक होता है।
- यह प्रमेय सर्किट के एक तत्व को एक और तत्व से बदल देता है।
- इस प्रमेय का उपयोग आश्रित स्रोतों वाले परिपथों का विश्लेषण करने के लिए किया जाता है।
किस परिपथ पर प्रतिस्थापन प्रमेय लागू नहीं होता है?
जिस परिपथ में उपरोक्त दो स्रोत हैं जो समानांतर या श्रृंखला में जुड़े हुए हैं, तो यह प्रतिस्थापन प्रमेय लागू नहीं होता है।
क्षतिपूर्ति प्रमेय को प्रतिस्थापन क्यों कहा जाता है?
मुआवजे और प्रतिस्थापन जैसे दोनों प्रमेय प्रक्रिया और कमी के संदर्भ में समान हैं। तो यह प्रमेय एंटेना के लिए लागू होता है और इसे प्रतिस्थापन प्रमेय भी कहा जाता है।
आप प्रतिस्थापन प्रमेय का उपयोग कैसे करते हैं?
इस प्रमेय का उपयोग पूरे नेटवर्क में वोल्टेज और धाराओं को परेशान किए बिना किसी नेटवर्क के भीतर एक अलग शाखा के साथ किसी भी शाखा को प्रतिस्थापित करके किया जा सकता है। अतः इस प्रमेय का प्रयोग रैखिक और अरेखीय दोनों परिपथों में किया जाता है।
प्रतिस्थापन संपत्ति क्या है?
प्रतिस्थापन गुण बताता है कि, यदि एक चर 'ए' दूसरे चर 'बी' के बराबर है, तो 'ए' को किसी भी अभिव्यक्ति या समीकरण में 'बी' के स्थान पर प्रतिस्थापित किया जा सकता है और 'बी' को 'बी' के स्थान पर प्रतिस्थापित किया जा सकता है। a' किसी भी व्यंजक या समीकरण में।
इस प्रकार, यह सब के बारे में है एक प्रतिस्थापन का अवलोकन प्रमेय - उदाहरण सहित परिपथ। यहां आपके लिए एक प्रश्न है, क्षतिपूर्ति प्रमेय क्या है?